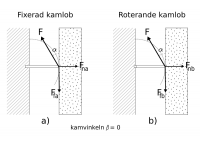
Varför har vi hittills jagat efter den magiska “normalkraften”? Borde inte den totala kraft som kilen/kammen överför till flaket/blocket vara mer relavant? Dvs, vi borde väl jämföra kraften K i Mezzners diagram av kammen (som överförs direkt till flaket/blocket till höger) med vektorsumman av N och myN i fallet med kilen?
först tänkte jag den komposanten som inte är normalkraft går ju parallellt med flaket, så den har ju ingen verkan.
sen tänkte jag att jag borde gä och lägga mig, men jag är snorig o hostig o kan inte sova ändå.
fast jag är väl snorig i räknehjärnan också, för jag fick ingen ordning på pilarna, utan försökte en annan variant:
om kammen har väldigt liten kamvinkel (kanske t.o.m. noll), och fixerade lober, då skulle den bete sig väldigt likt kilen - uttrycken för normalkraften bör då i så fall vara nära identiska, vilket inte stämmer med mezzners formler, inte heller med duracellkaninens (pga den omdiskuterade termen med friktionskraftbidraget), men däremot med achtminus ursprungliga uppställning (fast den var visst fel)
om kammen har rörliga lober (som sig bör), så är det frestande att tro att det kan tillkomma ett bidrag till normalkraften som har med kammens utväxling att göra, och med liten vinkel skulle den kunna vara rätt stor.
förutsatt att liten kamvinkel i en avsmalnande spricka är funktionellt ekvivalent med konventionell kamvinkel i en flärande spricka, vilket utan vidare inte är sant (utan formstöd behövs ju desto mer friktion som kammen behöver jobba upp).
så vilket spränger mest, en kam med fixerade lober, eller en med rörliga?
det sista jag tänkte innan jag gav upp var att normalkraften inte behöver vara större än att den resulterande friktionskraften håller kvar kammen i läge, så det kanske inte är någon skillnad?